이진 탐색 알고리즘이 다음의 수도 코드로 주어졌습니다.
BinarySearch(a[], key, left, right)
// a[mid] = key인 인덱스 mid를 반환
if (left <= right) then {
mid ← (left + right) / 2;
case {
key = a[mid] : return (mid);
key < a[mid] : return (BinarySearch(a, key, left, mid-1));
key > a[mid] : return (BinarySearch(a, key, mid+1, right));
}
}
else return -1; // key 값이 존재하지 않음
end BinarySearch()이 코드가 뭔지 분석하자는 말은 아니고, 단순히 복잡도 분석만 해보도록 하겠습니다.
참고로 수도 코드(pseudo code)란 실제 코드의 대략적인 기능만 써놓은 일종의 요약본 입니다.
먼저 이 BinarySearch 함수는 a[]라는 배열, key, left, right를 인자로 받습니다.
대충 이런 배열에 대해 BinarySearch라는 함수를 진행한다고 생각하시면 됩니다.

if문 안을 살펴보면, mid에는 left와 right의 중간 값이 저장됩니다.
그 아래를 보면 case가 세 개로 나뉩니다. if문 처럼 조건에 맞게 해당 내용을 실행하죠.
key = a[mid]일 때는 단순히 mid 값을 return하는데,
key < a[mid], key > a[mid]의 경우에는 BinarySearch 함수를 재귀호출 합니다.
근데 인자를 자세히 보면 key < a[mid]는 BinarySearch(a, key, left, mid-1),
key > a[mid]는 BinarySearch(a, key, mid+1, right)를 호출합니다.
대충 그림으로 본다면 전자는 초록색 배열에 대해 BinarySearch를 진행하고,
후자는 주황색 배열에 대해 BinarySearch를 진행한다고 생각하시면 됩니다. 물론 실제와는 좀 다르지만..

이렇게 되면 BinarySearch를 진행하는 데 절반의 시간이 걸린다고 봐도 되겠죠?
BinarySearch(a[], key, left, right)가 T(n)의 시간이 걸린다고 하면,
BinarySearch(a, key, left, mid-1)와 BinarySearch(a, key, mid+1, right)는 T(n/2)의 시간이 걸린다고 보는 겁니다.
이를 확인한 후 다시 BinarySearch 코드를 보겠습니다.
BinarySearch(a[], key, left, right)
// a[mid] = key인 인덱스 mid를 반환
if (left <= right) then {
mid ← (left + right) / 2;
case {
key = a[mid] : return (mid);
key < a[mid] : return (BinarySearch(a, key, left, mid-1));
key > a[mid] : return (BinarySearch(a, key, mid+1, right));
}
}
else return -1; // key 값이 존재하지 않음
end BinarySearch()최초에 T(n)의 복잡도를 갖는 BinarySearch를 호출하면, case에 따라 T(n/2)의 복잡도를 갖는 BinarySearch를 재귀호출 합니다.
또한 시간이 따로 들지 않는 연산이 함수 내에 있으면, 1의 시간을 가진다고 볼 수 있습니다.
따라서 위의 BinarySearch에선, T(n) = 1 + T(n/2)의 식을 세울 수 있습니다.
이처럼 점화식을 세우고, 시간 복잡도를 도출할 수 있습니다.
그렇다면 어떻게 구할 수 있는지 그 과정을 알아보겠습니다.
1. 식 세우기
2. 점화식 전개
우리는 방금 T(n) = 1 + T(n/2)의 식을 세웠습니다. 이를 점화 전개 해보면..
T(n) = 1 + T(n/2)
T(n/2) = 1 + T(n/2²)
T(n/2²) = 1 + T(n/2³)
∴ T(n) = 1 + 1 + 1 + T(n/2³)
3. i로 일반화
그렇게 얻은 2번에서의 식을 i로 일반화 합니다.
T(n) = i + T(n/2ⁱ)
4. 3번에서 얻은 우변의 T(@)에서 @=1일 때 i의 값 구하기
n/2ⁱ = 1 일 때, n = 2ⁱ , i = logn이 됩니다.
5. i를 대입하여 Tn 도출
T(n) = i + T(n/2ⁱ)에 n = 2ⁱ 와 i = logn을 대입하면,
T(n) = logn + T(1) 이 되며, T(1)은 매우 작은 시간이므로 소거한다면
T(n) = logn, 따라서 BinarySearch의 시간 복잡도는 O(logn) 이라는 결과가 나옵니다.
이러한 과정을 따르며 또 다른 문제도 해결해 보겠습니다.
만약 위의 BinarySearch에서 case문을 빼고 모든 경우에 BinarySearch(a, key, left, mid-1)와 BinarySearch(a, key, mid+1, right)가 둘 다 호출된다고 가정하면, 어떤 식을 세울 수 있을까요?
바로 T(n) = 1 + 2*T(n/2) 입니다.
이 점화식을 전개하면 다음과 같습니다.
T(n) = 1 + 2*T(n/2)
T(n/2) = 1 + 2*T(n/2²)
T(n/2²) = 1 + 2*T(n/2³)
∴ T(n) = 2² + 2 + 1 + 2³*T(n/2³)
i로 일반화까지 해주는데, 이 때 2ⁱ + .... + 2² + 2 + 1의 값은 등비수열의 합이므로 2 ⁱ - 1 이 됩니다.
따라서
T(n) = 2ⁱ - 1 + 2ⁱ * T(n/2ⁱ)
가 되며, n/2ⁱ = 1일 때 n = 2ⁱ , i = logn 이므로 이를 대입 해주면
T(n) = n-1 + n*T(1) = 2n-1 을 얻을 수 있고, 따라서 시간 복잡도는 O(n)이 나옵니다.
여러가지 경우에 따른 점화식을 더 살펴보겠습니다.
abc(n){
(~~ 1짜리 연산 ~~);
abc(n/2);
}이 경우 abc(n) 내부에 1짜리 연산 + 절반의 입력을 받는 재귀호출이 있으므로,
앞에서 했던 BinarySearch와 동일한 T(n) = T(n/2) + 1 입니다.
그림으로 확인하면, logn 층의 연산이 존재합니다.

abc(n){
for(~~);
abc(n/2);
}이 경우엔 1짜리 연산 대신 n의 시간이 걸리는 for 루프 하나가 들어갔으므로, T(n) = T(n/2) + n 입니다.
abc(n){
(~~ 1짜리 연산 ~~);
abc(n-1);
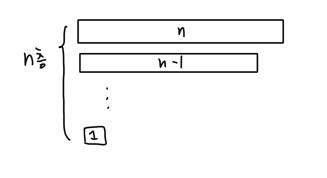
}이번엔 절반의 입력이 아닌, n-1개의 입력을 받는 재귀함수를 호출하므로 T(n) = T(n-1) + 1 입니다.
그림으로 확인하면, n층의 연산이 존재합니다.
abc(n){
for(~~);
abc(n-1);
}이것도 앞서 했듯 for 루프가 하나 들어갔으니 T(n) = T(n-1) + n 입니다.
그러나 이렇게 얻은 점화식을 복잡하게 전개하지 않고도 바로 복잡도를 알 수 있는 방법이 존재합니다.
다음 글에는 그 방법인 "마스터 정리(Master Theorem)"을 소개하겠습니다.
<틀린 점이 있다면 지적 부탁드립니다. 감사합니다.>
'전공 > C++' 카테고리의 다른 글
| 알고리즘 : 정렬 #2 (Mergesort, Quicksort, Stable) (0) | 2022.04.19 |
|---|---|
| 알고리즘 : 정렬 #1 (Bubble Sort, Insertion Sort, Selection Sort) (0) | 2022.04.19 |
| 알고리즘 : 마스터 정리(Master Theorem) (0) | 2022.04.18 |
| 알고리즘 : 복잡도(Big O notation, Omega notation) (0) | 2022.04.18 |
| 알고리즘 : 함수 호출과 재귀 함수, 복잡도 (0) | 2022.04.18 |








최근댓글