정렬 알고리즘(Sorting Algorithm)은 알고리즘 설계의 처음이자 마지막입니다.
정렬 알고리즘은 n개의 숫자가 주어졌을 때 이를 기준에 맞게 정렬하는 알고리즘으로, 개발자들은 지난 100년간 이 정렬 알고리즘의 실행 시간을 줄이기 위해 노력해왔습니다.
오늘 소개할 정렬은 제일 기본적인 정렬 세 가지입니다.
- Bubble Sort (버블 정렬)
- Insertion Sort (삽입 정렬)
- Selection Sort (선택 정렬)
위 세 가지 정렬은 모두 구조가 간단하며 O(n²)의 시간 복잡도를 가집니다.
따라서 잘 쓰이지는 않지만 다른 정렬의 기초가 되죠.
Bubble Sort (버블 정렬)
먼저 Bubble Sort(버블 정렬) 입니다.

이러한 크기 7 짜리의 배열 S가 있고, 우리는 이 배열을 작은 수부터 오름차순으로 정렬하려 합니다.
버블 정렬은 정말 단순하고 정직하게 끝에서부터 하나씩 대조하면서 작은 값을 위로 올립니다.
먼저 첫 단계에선 제일 끝의 6, 12를 비교하는데, 이미 작은 수가 위에 있으니 그대로 둡니다.

다음은 11과 6을 비교하여 6을 위로 올려줍니다.

이렇게 자리바꿈을 하는데엔 먼저 if 문으로 두 숫자의 대소를 비교한 뒤, 밑에 있는 수가 작다면 자리를 바꿔주기 위해서 swap 함수를 넣거나 그와 같은 기능을 하는 코드가 필요하겠죠.
계속해서 같은 행동을 수행합니다.

그렇게 되면 제일 작은 값인 3이 가장 위로 올라오며, 정렬이 완료된 숫자로 처리됩니다.
이제 해야할 것은 뭘까요? 바로 배열의 2~7 번째 원소의 정렬입니다.
2~7번째 원소를 정렬해서 6을 정렬이 완료되었다고 처리하면, 또 남은 3~7번째 원소를 정렬합니다.
이렇게 모든 숫자가 정렬되도록 하면 Bubble Sort가 끝이 납니다.

마지막으로 Bubble Sort의 코드를 확인하겠습니다. 위에서 설명한 기능대로 돌아가도록 작성했습니다.
void bubblesort(int n, int S[]) {
int i, j, temp;
for (i = 1; i <= n - 1; i++)
for (j = n-1; j > 1; j--)
if (S[j] < S[j - 1]) {
temp = S[j];
S[j] = S[j - 1];
S[j - 1] = temp;
}
}
int main() {
const int n = 8;
int S[n] = { NULL, 13, 7, 9, 3, 11, 6, 12 };
bubblesort(n, S);
for (int i = 1; i < n; i++)
cout << S[i] << " ";
}참고로, 배열을 생성하면 첫 칸이 0번 인덱스임은 다 아실텐데, 위의 코드는 직관적으로 i번째 칸과 j번째 칸을 swap.. 이라는 식으로 작성한 코드이므로, 0번 인덱스는 NULL 값이고 1번부터 정렬을 시작하는 배열이라고 생각하시면 됩니다.
if 절에는 비교 연산을 1회, 또 S[j]와 S[j-1]을 바꾸는 swap 에서 3번의 "=" 연산이 들어 있습니다.
그리고 이 연산을 이중 for 루프가 감싸고 있으니, 총 비교는 n²번, "=" 연산은 3n²번이 일어납니다.
또한 추가적인 배열을 쓰지 않고 S 배열 내에서만 자리를 바꾸는데, 이것을 제자리정렬(In-place) 이라고 합니다.
Insertion Sort (삽입 정렬)
다음으로 Insertion Sort(삽입 정렬) 입니다.
이 정렬은 먼저 배열의 제일 앞에 있는 수를 이미 정렬된 배열이라고 봅니다.
그리고 정렬이 안 된 나머지를 차례대로 정렬된 배열 속에 대소를 비교하면서 삽입합니다.
말로는 뭔지 모르겠는데... 그림을 보시면 한번에 이해가 가실 겁니다.

제일 앞에 있는 13을 이미 정렬된 배열이라고 보고, 그 아래 7부터 12를 차례대로 이 배열에 집어넣을 겁니다.
먼저 7을 넣을건데, 그림을 보시면 7은 13의 앞, 뒤에 삽입할 수 있겠죠? 이 때 7은 13보다 작으므로 앞에 넣어줍니다.
그러면 이젠 이미 정렬된 배열에 7, 13이 있게 되죠.
이제 똑같이 9도 넣어줍니다.

9도 그림의 ☆ 자리에 삽입할 수 있는데, 앞에서부터 대소비교를 하면 중간에 들어갑니다.
계속해서 3도 넣어주겠습니다.

3이 들어갈 ☆의 선택지는 4곳입니다. 일단 3<7 이므로 첫 대소비교 만에 자리가 결정되네요.
하지만 숫자가 크다면 어떻게 될까요? 알고리즘이 배열의 처음부터 대소비교를 하도록 짜여있다고 합시다.

3의 경우엔 첫 비교 만에 자리가 결정되어 1번의 연산만 하고 넘어갑니다.
그러나 8이 온다면 7과 8, 8과 9를 비교해야 위치가 결정되므로 2번의 연산만에 자리가 정해집니다.
12가 온다면 (7,12), (9,12), (12,13) 총 세 번의 비교 연산을 마쳐야 자리가 정해지네요.
13보다 큰 15가 와도 (7,15), (9,15), (13,15) 세 번의 연산만 필요한데, 이는 13보다 작으면 ☆3, 13보다 크면 ☆4 위치로 가는 것이 세 번째 연산에서 결정되기 때문입니다.
따라서 지금 단계에서는 세 번의 연산을 다 하는 경우가 worst case라고 볼 수 있습니다.
이를 주어진 i에 대해 최대 i-1번의 비교가 일어난다고 하는데, 코드를 보면서 말씀드리겠습니다.
void insertsort(int n, int S[]) {
int i, j, x;
for (i = 2; i < n; i++) {
x = S[i];
j = i - 1;
while (j > 0 && S[j] > x) {
S[j + 1] = S[j];
j--;
}
S[j + 1] = x;
}
}
int main() {
const int n = 8;
int S[n] = { NULL, 13, 7, 9, 3, 11, 6, 12 };
insertsort(n, S);
for (int i = 1; i < n; i++)
cout << S[i] << " ";
}insertsort가 실행되고 for문 첫 바퀴에서 while문에 들어가기 직전 상태입니다.
i=2로 시작해서 x에 S[i]의 값인 7을 저장해 두고, j에 1을 저장합니다.
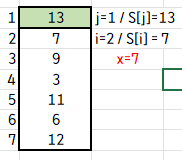
j>0 이고 S[j]가 x(=S[i])보다 크므로 while문의 조건을 충족하므로 while문을 진행합니다.
S[j+1]에 S[j]의 값을 저장하죠. 여기서 S[j+1] = S[i] 입니다. 그러고선 j--를 진행합니다.
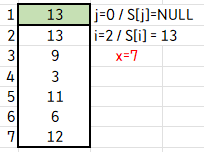
다음으로 S[j+1]에 x 값을 저장합니다.
아까 j--를 해주었으니 j=0이고, S[j+1] = S[1]에 7을 저장하게 되면 swap이 완료됩니다.
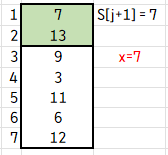
방금 알아본 첫 번째 삽입에서 i=2 임을 확인할 수 있었습니다.
그렇다면 아까 최대 3번의 비교가 일어난다고 하였던 3번째 삽입에서는 i=4가 되므로,
주어진 i에 대해 최대 i-1번의 비교가 일어남을 확인 가능합니다.
Insertion Sort는 for 루프 안에 while문이 있는 이중 반복문 안에 비교 연산자와 "=" 연산자가 1번 들어갑니다.
따라서 "=" 의 총 연산횟수는 n²회이며, 시간 복잡도는 O(n²) 입니다.
또한 정렬하는 데 추가적인 배열이 필요하지 않으므로 Insertion Sort도 제자리 정렬입니다.
Selection Sort (선택 정렬)
마지막으로 Selection Sort(선택 정렬) 입니다.
Selection Sort는 하나의 값을 선택하여 최소값이라고 가정한 뒤, 나머지를 scan하면서 가장 작은 값을 찾아 교환합니다.
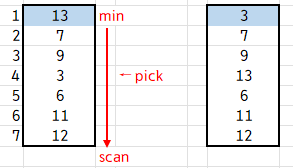
첫 인덱스에 있는 13을 무작정 최소값이라고 가정하고,
7부터 12를 scan 한 뒤 그중에서 가장 작은 값인 3과 교환합니다.
그렇게 되면 3은 정렬이 끝났고, 이젠 7을 최소값이라 가정하고 9부터 12를 scan 합니다.
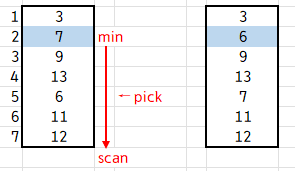
이런 식으로 끝까지 정렬하는 게 Selection Sort 입니다.
코드를 확인하도록 합시다.
void selectionsort(int n, int S[]) {
int i, j, min, temp;
for (i = 1; i < n-1; i++) {
min = i;
for (j = i + 1; j < n; j++)
if (S[j] < S[min])
min = j;
temp = S[i];
S[i] = S[min];
S[min] = temp;
}
}
int main() {
const int n = 8;
int S[n] = { NULL, 13, 7, 9, 3, 11, 6, 12 };
selectionsort(n, S);
for (int i = 1; i < n; i++)
cout << S[i] << " ";
}첫 번째 for 루프에서 내부 for 문을 막 들어와서 j=i+1의 값을 받은 상태입니다.
지금은 i=1, min=1, j=2의 값을 가집니다.

if절의 조건인 S[j] < S[min] 에 맞으므로 min = j 를 진행합니다. 따라서 min에는 2가 저장됩니다.

그 다음 루프(j=3)에선 S[j] < S[min] 이 참이 아니라 if절을 진행하지 않고 다음 루프를 진행합니다.
min에는 계속 2가 저장되어있습니다.
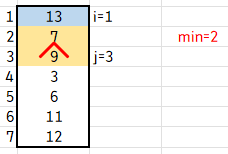
j=4인 루프에선 S[j] < S[min]을 만족하므로, if절을 진행합니다. 따라서 min에는 4가 저장됩니다.

이렇게 12까지 스캔을 하게 되면 min에는 최종적으로 4가 저장됩니다.
마지막 swap 문으로 S[i]와 S[min]을 서로 바꿔주면 첫 번째 루프가 끝이 납니다.
Selection Sort는 내부 for문에 "=" 연산이 1회, 외부 for문에 "=" 연산이 3회 있습니다.
"=" 연산이 총 n²+3n회 이뤄지므로 시간 복잡도는 O(n²) 입니다.
또한 정렬하는 데 추가적인 배열이 필요하지 않으므로 Selection Sort도 제자리 정렬입니다.
<틀린 점이 있다면 지적 부탁드립니다. 감사합니다.>
'전공 > C++' 카테고리의 다른 글
| 알고리즘 : 정렬 #3 (Shell Sort, Heap Sort) (0) | 2022.04.20 |
|---|---|
| 알고리즘 : 정렬 #2 (Mergesort, Quicksort, Stable) (0) | 2022.04.19 |
| 알고리즘 : 마스터 정리(Master Theorem) (0) | 2022.04.18 |
| 알고리즘 : 복잡도의 점화식 (0) | 2022.04.18 |
| 알고리즘 : 복잡도(Big O notation, Omega notation) (0) | 2022.04.18 |








최근댓글