이번에 알아볼 것은 Mergesort(합병 정렬), In-place Quicksort(제자리 퀵 정렬)이며, 정렬의 Stable함을 소개하며 마치겠습니다.
Merge Sort (합병 정렬)
Mergesort에 들어가기 전, 저번에 복잡도의 점화식에 대해 소개할 때 이상한 코드 하나를 가져왔었죠?
BinarySearch(a[], key, left, right)
// a[mid] = key인 인덱스 mid를 반환
if (left <= right) then {
mid ← (left + right) / 2;
case {
key = a[mid] : return (mid);
key < a[mid] : return (BinarySearch(a, key, left, mid-1));
key > a[mid] : return (BinarySearch(a, key, mid+1, right));
}
}
else return -1; // key 값이 존재하지 않음
end BinarySearch()바로 이 코드입니다.
그 때 말했듯 이 함수를 실행하면 절반짜리 입력으로 재귀호출을 한다고 했죠.
본론으로 들어와서, Mergesort(합병 정렬)는 위의 BinarySearch 처럼 절반짜리 입력으로 재귀호출합니다.
먼저 Mergesort의 알고리즘을 살펴보겠습니다.
void mergesort (int n, keytype S[]) {
const int h = n / 2, m = n - h;
keytype U[1..h], V[1..m];
if (n > 1) {
copy S[1] through S[h] to U[1] through U[h];
copy S[h+1] through S[n] to V[1] through V[m];
mergesort(h,U);
mergesort(m,V);
merge(h,m,U,V,S);
}
}
여기 크기 n을 갖는 배열 S가 있습니다.
mergesort의 초반에 보시면 h = n/2, m = n-h, 또 배열 U와 V를 정의합니다.

배열 U와 V의 크기를 합치면 S의 크기와 같은 n이 되죠.
그런데 if절 안으로 들어가보면, S의 내용을 U와 V에 복사합니다.

이런 식의 배열이 만들어지는 거죠.
그 다음엔 배열 U와 V에 대해 mergesort를 재귀호출합니다. 아까 BinarySearch처럼 입력의 크기가 절반입니다.

이 다음엔 계속된 재귀호출로 한조각씩 나눠진 배열을 정렬하면서 합치는 merge 함수를 호출하는데, 일단 이 함수의 연산 횟수가 n이라고만 생각하고 넘어갑시다.
case에 따라 나뉘어 하나만 재귀호출 하여 T(n) = T(n/2) + 1 이었던 BinarySearch와 달리,
mergesort는 조건문 없이 둘 다 호출하고 덤으로 merge 함수도 호출하니 T(n) = 2*T(n/2) + n 이라고 볼 수 있습니다.
이를 점화전개로 풀거나 마스터 정리로 풀어보면 T(n) = O(nlogn) 을 구할 수 있습니다.
방금 언급한 merge 함수의 알고리즘도 살펴보겠습니다.
void merge(int h, int m, const keytype U[], const keytype V[], const keytype S[]) {
index i, j, k;
i = 1; j = 1; k = 1;
while (i <= h && j <= m) {
if (U[i] < V[j]) {
S[k] = U[i];
i++;
}
else {
S[k] = V[j];
j++;
}
k++;
}
if (i > h)
copy V[j] through V[m] to S[k] through S[h+m];
else
copy U[i] through U[h] to S[k] through S[h+m];
}앞서 말했듯 merge 함수는 정렬하면서 합치는 기능을 합니다.
여기 U와 V 배열을 정렬하면서 합쳐 S 배열을 만들려고 하는데... 어떻게 하는 걸까요?

먼저 merge 함수는 U의 크기 h, V의 크기 m, 배열 U, V, S를 인자로 받습니다.
첫 시작은 h=3, m=5, i=1, j=1, k=1로 시작하고, while문을 맞닥뜨립니다.
(i<=h && j<=m) 이라는 조건은, i가 h를 넘기거나, j가 m을 넘기면 루프를 종료한다는 뜻이라고 볼 수 있습니다.
while문 안으로 들어가서 if절을 살펴보겠습니다. U[i]와 V[j]를 비교해서,
U[i] < V[j]면 S[k]에 U[i]의 값을 저장하고 i++ 하며,
U[i] ≥ V[j]면 S[k]에 V[j]의 값을 저장하고 j++ 합니다. 그 후 k를 1 증가하면서 if절을 끝냅니다.
그림으로 확인해 보겠습니다.

U[1] < V[1] 이므로 S[1]에 U[1]의 값을 저장하고 i와 k를 1 증가합니다.
그렇게 되면 i=2, j=1, k=2의 값을 가지죠.

이번에는 U[2] > V[1] 이므로 S[2]에 V[1]의 값을 저장하고 j와 k를 1 증가합니다.
이런 식으로 계속 S에 값을 넣어보겠습니다.
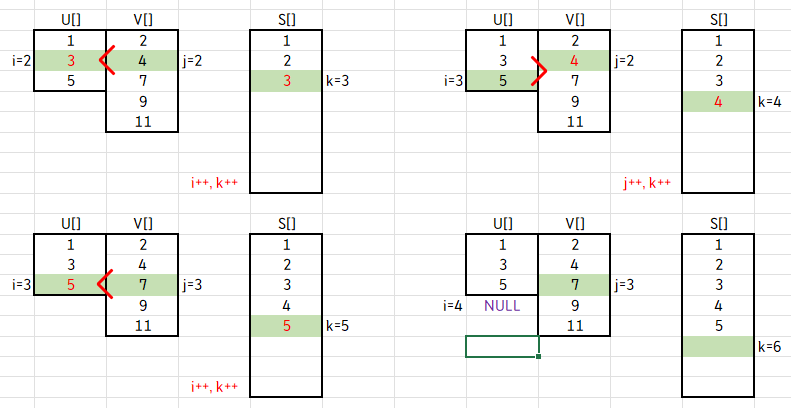
계속 진행하다 보면, 앞서 말했던 while문의 조건에 어긋나는 경우가 생깁니다.
이번 경우엔 i=4가 되어 h=3 보다 큰 값을 갖게 되므로 while문을 탈출하게 됩니다.
while문을 벗어나면, if 절이 있습니다.
i > h 면 V[j] ~ V[m] 을 S[k] ~ S[h+m]에 복사하거나,
j > m 이면 U[i] ~ U[h] 를 S[k] ~ S[h+m]에 복사합니다.
즉, while문을 벗어난 후에 U나 V 중 값이 남아있는 배열이 있으면 그 값을 그대로 S에 복사한다는 뜻입니다.
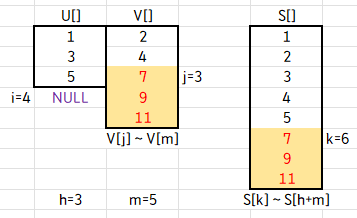
이렇게 merge 함수가 종료됩니다.
MergeSort의 전체 코드는 다음과 같습니다.
void merge(int h, int m, const int U[], const int V[], int S[]) {
int i = 1, j = 1, k = 1;
while (i <= h && j <= m) {
if (U[i] < V[i]) {
S[k] = U[i];
i++;
}
else {
S[k] = V[j];
j++;
}
k++;
}
if (i > h) {
for (int idx = j; idx <= m; idx++) {
S[k] = V[idx];
k++;
}
}
else {
for (int idx = i; idx <= h; idx++) {
S[k] = U[idx];
k++;
}
}
}
void merge_sort(int n, int S[]) {
const int h = n / 2, m = n - h;
int* U = new int[h + 1];
int* V = new int[m + 1];
if (n > 1) {
for (int i = 1; i <= h; i++) U[i] = S[i];
for (int i = 1; i <= m; i++) V[i] = S[i + h];
merge_sort(h, U);
merge_sort(m, V);
merge(h, m, U, V, S);
}
delete[] U;
delete[] V;
}
쪼개고, 쪼개고, 또 쪼개고, ... 끝까지 쪼갠 다음 정렬하면서 합치고, 정렬하면서 합치고, ...
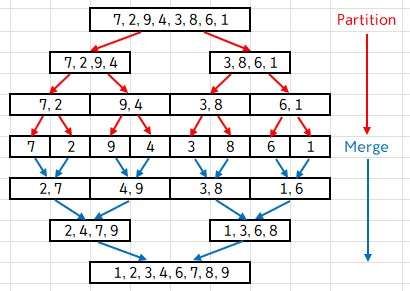
이 과정이 Mergesort라고 할 수 있겠습니다.
앞서 Mergesort의 시간 복잡도는 T(n) = O(nlogn) 임을 확인했습니다.
그러나 U, V 배열을 추가로 만들어줘야 하므로, Mergesort는 제자리 정렬이 아닙니다.
Quick Sort (퀵 정렬)
이번엔 Quicksort(퀵 정렬)에 대해 알아보겠습니다.
퀵 정렬은 "pivot"이라는 랜덤한 원소를 선택하고, 이 원소를 기준으로 작으면 왼쪽, 크면 오른쪽으로 나눕니다.
그렇게 나눈 배열에서도 pivot을 선정하여 계속해서 정렬하는 것이 Quicksort 입니다.
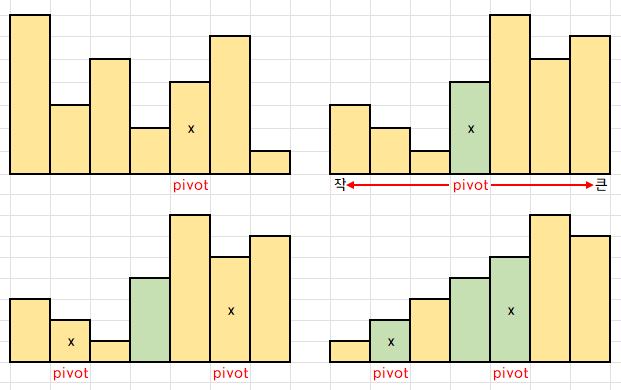
이런 Quicksort 또한 단점이 존재합니다. 배열 S가 다음과 같다고 합시다.

이 때 pivot을 선정하고, 새 배열 U를 만듭니다.
S[0]부터 pivot과 대소비교를 하면서 작은 값은 U 배열의 왼쪽, 큰 값은 오른쪽부터 차곡차곡 넣습니다.

이렇게 정렬하고 pivot을 제외한 양 옆의 배열을 재귀호출하여 정렬하는 것이 퀵 정렬인데,
이 방법은 Mergesort 처럼 추가로 배열이 필요합니다.
하지만 개발자들의 머리는 우리가 생각한 것보다 더 괴물이었죠.
추가로 배열을 만들지 않고도 정렬할 수 있는 In-Place Quicksort(제자리 퀵 정렬)를 고안해 냅니다.
먼저 In-Place Quicksort의 알고리즘을 확인하겠습니다.
Algorithm inPlaceQuickSort(S, a, b)
if a >= b then return
p ← S.elemAtRank(b)
l ← a
r ← b-1
while (l <= r)
{
while (l <= r and S.elemAtRank(l) <= p)
l++;
while (l <= r and S.elemAtRank(r) >= p)
r--;
if (l < r)
S.swap(S.atRank(l), S.atRank(r));
}
S.swap(S.atRank(l), S.atRank(b));
inPlaceQuickSort(S, a, l - 1)
inPlaceQuickSort(S, l + 1, b)inPlaceQuickSort 함수는 인자로 배열 S와 a, b를 갖습니다.
여기서 a는 배열의 제일 첫 인덱스를 가리키는 포인터, b는 배열의 제일 끝 인덱스를 가리키는 포인터 입니다.
배열 S가 다음과 같다고 합시다.
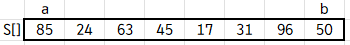
p ← S.elemAtRank(b)가 바로 pivot을 선정하는 pivotting 인데, 제일 끝의 원소를 pivot으로 선정합니다.
따라서 p에는 b가 가리키는 인덱스의 원소인 50이 저장되겠죠.
그리고 l 포인터, r 포인터를 정의하면 다음 그림과 같아집니다.
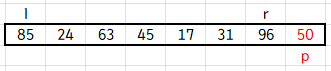
이 상태에서 while 문으로 들어가겠습니다.
이 while문의 조건은 l <= r, 즉 l > r 이 되면 while문을 탈출합니다. 이를 기억해두세요.
들어가서 내부의 while문을 살펴보면,
l <= r and S.elemAtRank(l) <= p 조건을 갖추면 l++을 하고,
l <= r and S.elemAtRank(r) >= p 조건을 갖추면 r--를 해준답니다.
이를 풀어서 설명하면, l이 가리키는 값이 p보다 작으면 l 포인터를 오른쪽으로 이동하고,
r이 가리키는 값이 p보다 크면 r 포인터를 왼쪽으로 이동한다는 뜻입니다. 그림으로 살펴보겠습니다.

지금은 l이 가리키는 값이 p보다 크므로, 내부 while문을 탈출합니다. 즉 l 포인터를 멈춥니다.
r이 가리키는 값은 p보다 크므로, r-- 를 해주어 r 포인터를 왼쪽으로 이동합니다.
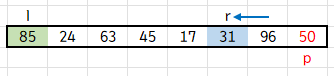
r이 가리키는 값이 p보다 작으므로, 내부 while문을 탈출하여 r 포인터를 멈춥니다.
이렇게 내부 while문을 빠져나왔을 때 l < r 이면 l이 가리키는 값과 r이 가리키는 값을 swap 해줍니다.
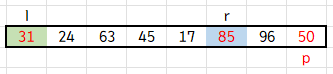
또 다시 l 포인터는 오른쪽, r 포인터는 왼쪽으로 옮겨갑니다.

이번에는 l이 p보다 큰 63을 만나서 멈추고, r이 p보다 작은 17을 만나 멈춥니다. 또 둘을 swap 해줍니다.

그리고 계속 진행하다보면...

이렇게 r과 l이 교차하게 됩니다. 앞서 기억해놓으라 했던 l > r 이 되는 경우이죠.
이 때 외부 while문을 탈출합니다.
탈출하고 나면 S.swap(S.atRank(l), S.atRank(b))를 맞닥뜨리는데,
l이 가리키는 값과 b가 가리키는 값을 swap 해줍니다.
b가 가리키는 값은 pivot 이므로, 바꾸게 되면..
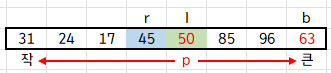
놀랍게도 pivot보다 작은 값은 왼쪽, 큰 값은 오른쪽에 정렬됩니다. 이 때 pivot인 50은 자기 자리를 찾았습니다.
추가로 배열을 만들지 않고도 정렬을 해버린 것이죠.
그 다음엔 inPlaceQuickSort(S, a, l - 1); inPlaceQuickSort(S, l + 1, b); 로 재귀호출 해줍니다.

자기 자리를 찾은 50을 제외한 양 옆의 배열에서 또 위와 같은 과정을 해 주는 겁니다.
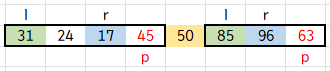
이렇게 계속 재귀호출을 해주며 정렬하면 추가 배열이 필요 없는 In-Place Quicksort가 끝납니다.
그러나 In-Place Quicksort에도 단점은 존재합니다.
Quicksort 자체의 단점이라고 봐도 좋은데, 바로 pivotting을 잘못하면 시간 복잡도가 O(n²)까지 악화됩니다.
pivot으로 정한 맨 끝의 값이 운 없게도 제일 큰 값이고, 또 다음 재귀호출 때도 제일 큰 값을 골라버리고, ...

그렇게 맞이한 최악의 상황(worst case)에는 O(n²)까지 악화됩니다.
반면 pivotting을 기깔나게 잘 선택해서 고르는 족족 중간값이 나온다면 최상의 상황(best case)이겠죠?
이 때는 T(n) = T(n/2) + T(n/2) + n 으로, 정리하면 T(n) = O(nlogn) 이 나옵니다.
따라서 Quicksort의 시간 복잡도는 경우에 따라 O(nlogn)부터 O(n²)까지로 볼 수 있습니다.
평균을 내보면 대충 1.38nlogn 이라고 하네요.
대체로 pivot을 찍었을 때 Quicksort가 잘 동작할 확률은 pivot 값으로 중간 언저리의 값을 선택한 1/2 확률입니다.
그런데, 여러가지 방법으로 이 Quicksort의 성능을 향상시킬 수 있습니다.
1. 스택을 사용하여 순환을 제거
2. 작은 부분 화일
3. 중간값 분할
먼저 스택을 사용해서 재귀호출을 없애는 방법인데, 이는 또 스택이 필요하게 됩니다.
그럼에도 불구하고 원래의 Quicksort보다 빠르다고 하네요.
그리고 두 번째 방법인 작은 부분 화일은, 부분으로 나온 배열(부분 화일)이 일정 크기 이하로 작아지면 그 때부턴 Quicksort가 아닌 Insertion sort, 즉 삽입정렬을 수행합니다.
if (b-a <= M) InsertionSort(S, a, b);n이 작으면 차라리 Insertion sort를 쓰는게 더 빠르다고 합니다.
마지막 방법은 중간값 분할입니다. 제일 좋은 방법이라고 하는데, 바로 pivotting을 효율적으로 하는 겁니다.
m = (a + b) / 2;
if (S[a] > S[m]) swap(S, a, m);
if (S[a] > S[b]) swap(S, a, b);
if (S[m] > S[b]) swap(S, m, b);
swap(S, m, b);
p ← S.elemAtRank(b);p ← S.elemAtRank(b) 하기 전, 3개의 원소를 임의로 선택합니다. 보통은 양 끝값과 가운데 값을 선택합니다.
그리고 그 선택한 세 원소를 대소비교 하여 중간값을 pivot으로 선정하는 겁니다.
그 중간값을 pivot으로 선정하려면, 이 중간값이 b가 가리키는 위치로 오도록 swap 해준 뒤
b가 가리키는 값을 p ← S.elemAtRank(b)으로 pivotting 해 줍니다.
Stable
마지막으로 정렬의 stable함에 대해 알아보겠습니다.
stable이란, 중복된 key값이 있을 때, 정렬 전과 정렬 후에 해당 key의 순서가 바뀌지 않는 상태 입니다.
다음 표를 학년에 따라 정렬하려고 합니다.
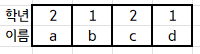
이 때, 1을 중복으로 가진 b, d와 2를 중복으로 가진 a, c의 이 순서가 정렬 후에도 유지되는 것이 stable 입니다.
Selection sort(선택정렬)로 한번 정렬 해 보겠습니다.

정렬 전에는 1은 b, d, 2는 a, c의 순서였는데, 정렬 후에는 2가 c, a 순서로 뒤바뀌었습니다.
따라서 Selection sort는 stable 하지 않습니다.
정렬 알고리즘의 특징을 정리한 표를 보여드리며 마치겠습니다.
| Algorithm | Time | Stable | In-place |
| Bubble Sort (버블 정렬) |
O(n²) | O | O |
| Insertion Sort (삽입 정렬) |
O(n²) | O | O |
| Selection Sort (선택 정렬) |
O(n²) | X | O |
| Merge Sort (합병 정렬) |
O(nlogn) | O | X |
| Quick Sort (퀵 정렬) |
O(nlogn) | O | X |
| In-place Quick Sort (제자리 퀵 정렬) |
O(nlogn) | X | O |
<틀린 점이 있다면 지적 부탁드립니다. 감사합니다.>
'전공 > C++' 카테고리의 다른 글
| 알고리즘 : 스트링 탐색 #1 (Naive, 직선적 알고리즘) (0) | 2022.05.17 |
|---|---|
| 알고리즘 : 정렬 #3 (Shell Sort, Heap Sort) (0) | 2022.04.20 |
| 알고리즘 : 정렬 #1 (Bubble Sort, Insertion Sort, Selection Sort) (0) | 2022.04.19 |
| 알고리즘 : 마스터 정리(Master Theorem) (0) | 2022.04.18 |
| 알고리즘 : 복잡도의 점화식 (0) | 2022.04.18 |








최근댓글